We are innately averse to pain as human beings. If we burn our hands on the stove, we learn to never put our hands on the stove again.
This is part of the reason of why it is so difficult to become a successful long term investor – over a long period of time, the likelihood of anyone losing money is almost a foregone certainty. No one has ever entered the markets and not lost money to it.
Such a problem becomes exacerbated when you consider how to teach an Early Retirement Masterclass. Retirement entails relying on dividends/bonds for the long term where the retiree is almost always jobless whether by choice or by circumstance. This means losses in the stock market can be perceived to be even more worrying or painful.
So how do we ensure that students are able to withstand, or at least mitigate the negative impact of losing money when it is almost an utter certainty the longer they stay in the market?
The answer to such a question can be found in the simple application of statistics, and performance psychology.
In Performance Psychology, having self-efficacy, a concept developed by psychologist Albert Bandura in 1971, is defined as having beliefs in one’s capabilities to organize and execute the course of action required to produce given attainments.
The ideal course participant is someone who can organise and execute an investment plan – after attending a course, a person should be able to construct a portfolio that will eventually be able to extract dividend payments within three months of attending class.
The biggest source of self-efficacy comes from mastery experiences, this is where the successful experience of performing a task leads to a positive experience that, in turn, reinforces a person’s efficacy beliefs that spur further action.
Think of the first time you rode a bicycle, learned to swim or learned to climb the stairs as a toddler. Each time you successfully carried out such actions led to the buildup of an experience that gave you greater confidence in carrying out future actions.
A beginning investor can thus. “level up”, if he or she can receive enough positive experiences to spur him on to read and devote more study on the financial markets.
Applying Theory to Practice
With this in mind, let’s examine the learning process of a self-taught retail investor who decides to test the waters using the STI ETF. When back-tested this month, the Straits Times Index Exchange Traded Fund returned 6.61% with a semi-variance of 10.87% over the past 10 years.
If you remember how to use a normal distribution table in your statistics classes in secondary school, using a Z-score of -6.61 / 10.87 or approximately -0.61, there is a 27.09% chance of incurring a loss in your first year as an investor.
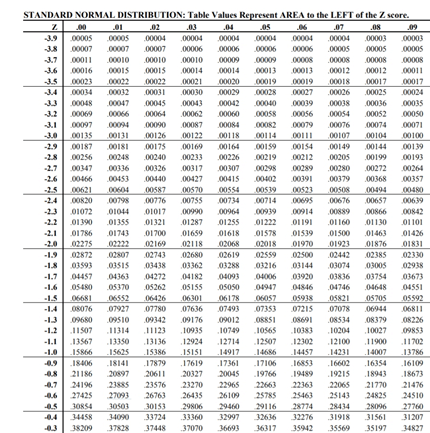
What this means is that for each batch of self-learners, there is a 27.09% chance that they may have their confidence shaken when they begin investing.
A significant number of these rookies may quit investing after this because we have evolved from our ancestors with an aversion to losses. It is human nature to give up on the stock market after getting burned after one or two bad trades.
This is the reason why a starter portfolio cannot afford to devolve to market returns. The dropout rate can be larger than a quarter of folks who give it a try.
But a savvy retail investor can do better.
If you learn to employ high dividend yield blue-chips when investing in local blue-chips. Shortlisting 15 of the blue-chip stocks that gives the highest dividend yields can produce better returns of 8.4% with a semi-variance of 10.79%.
With a Z-score of -8.8 / 10.79, we get -0.82. Referring to the table, we can reduce the probability of losing money to 20.6%. I would take that 7% edge of not losing money every day of the week – there is no downside to this. This is the beauty of understanding how to look at the markets statistically. Subjectivity is reduced.
This is a much better way to cultivate self-efficacy for rookie investors. The added benefit of seeing dividends arrive in your bank account can also be a morale booster.
Beginning investors need an equity portfolio that will minimise the odds of losing money in any particular year to prevent the likelihood of them quitting early – if not, they will never become successful long term investors, and their course fees would have been paid for nothing. We can’t help them invest after all.
The ERM Masterclass employs a top-of-the-line strategy that was back-tested to return 15.58% with a semi-variance of 8.63% for the past 10 years. The Z score thus becomes -1.81 (a result of -15.58/8.63). This means that your odds of losing money drops to 3 and a half times out of every 100 times.
Further, this model produces a dividend yield of 6.37% producing a nice dopamine rush that can motivate you to take further action once every quarter.
In summary, the course design is a multi-disciplinary affair. The ultimate aim in course design is to develop the self-efficacy of rookie retail investors so that they can be motivated to push their financial mastery into greater heights.
The odds of developing self-efficacy, however, is limited by the statistical properties of a rookie portfolio that will be deployed into the markets.
Self-study and experimentation are good, but an approach that provides a beginning investor with a safer starter portfolio will give you more mileage in your journey towards greater financial expertise.
A good course also allows you to develop more self-efficacy by vicariously experiencing the success of your classmates and the gentle prodding and persuasion of an instructor.
If nothing else, at least you would have learnt from reading this article that the tables you used to reference in your H2 Mathematics A level exams have practical use in investment portfolio design.
If you’d like to find out more about the early retirement masterclass, you can do so here.

